Use of Rmarkdown: taking GFM package as an example
Introduction of Rmarkdown
In this section, we briefly introduce some features of Rmarkdown.The Laguage of Rmarkdown is similar to that of Markdown, which is very easy to learn and write it.
Creating Rmarkdown file in Rstudio
Firstly, we create a new file in Rstudio, then choose the format of this file as ‘Rmd’(extension name). If we uncarefully save it as format ‘md’, then we can not run R code in each small chunk. Second, we need to set the header, including ‘title’, ‘author’, ‘date’, ‘output’, where title is the title of this document, ‘author’ and ‘date’ are the author and created date of this document, ‘output’ specifies the information about the output file. As for output file, we can generate three types of files, including ‘html’, ‘word’ and ‘pdf’, whose setting can be done in the setting whidow of ‘Knit’. The following is an example of header of this file.
title: "Use of Rmarkdown: taking GFM package as an example"
author: "Wei Liu"
date: '2020-11-23'
output:
pdf_document:
highlight: kate
number_sections: yes
toc: yes
word_document:
toc: yes
html_document:
fig_caption: yes
highlight: pygments
theme: cerulean
toc: yesAftering finishing the setting, we can arbitrarily write our contents of document. If any problem about the statements, we can turn to Baidu, Biying or Google!
R package GFM
In this section, we provide an inroduction to the GFM package, which is available at . R package GFM implements GFM, the generalized factor models for utra-high-dimensional mixed correlated data. It is more powerful than linear factor analysis, since it can handle mixed data, achieve nonlinear feature extraction and have theoretical guarantee. We can install the package from github by using following codes.
library(devtools)
install_github("feiyoung/GFM")Load the package using the following command:
library(GFM)GFM feature extraction using simulated data
In the following, we give some examples with different variable types. ### Homogeneous continuous variables We first generate data with homogeneous normal variables from the following model \[x_{ij}= \mu_j + h_i b_j^T + u_{ij}, \] where \(u_{ij} \sim N(0, \sigma^2)\), which can be generated by function gendata:
n <- 100
p <- 100
q <- 2; rho <- 3
dat <- gendata(q = q, n=n, p=p, rho=rho)
str(dat)## List of 4
## $ X : num [1:100, 1:100] -0.5488 1.4796 0.0512 0.2888 -0.831 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : NULL
## .. ..$ : NULL
## $ B0 : num [1:100, 1:2] 0.1991 -0.0584 0.2656 -0.5071 -0.1047 ...
## $ H0 : num [1:100, 1:2] -0.148658 -0.000162 -0.098823 1.02493 0.628709 ...
## $ mu0: num [1:100] 0.164 0.676 0.635 -0.132 -0.914 ...In the above commands, n is the sample size, p is the variable dimension, q is the number of factors, \(\rho\) controls the signal strength. We can refer to the help file using
?gendatafor more details.
Then we fit the GFM model by following commands:
group <- rep(1,ncol(dat$X))
type <- 'gaussian'
# specify q=2
gfm1 <- gfm(dat$X, group, type, q=2, output = F)## Starting the alternate minimization algorithm...
## Finish the iterative algorithm...str(gfm1)## List of 6
## $ hH : num [1:100, 1:2] 0.198 -0.324 0.47 0.653 0.317 ...
## $ hB : num [1:100, 1:2] 0.1963 -0.169 0.1607 -0.4243 -0.0848 ...
## $ hmu : num [1:100] 0.259 0.684 0.638 -0.191 -0.877 ...
## $ obj : num 0.966
## $ q : num 2
## $ history:List of 7
## ..$ dB : num [1:3] 1 0.01765 0.00541
## ..$ dH : num [1:3] 0.0558 0.01407 0.00493
## ..$ dc : num [1:3] 1.00 1.13e-04 6.29e-05
## ..$ c : num [1:3] 0.966 0.966 0.966
## ..$ realIter : num 3
## ..$ maxIter : num 50
## ..$ elapsedTime: 'proc_time' Named num [1:5] 0.09 0.02 1.75 NA NA
## .. ..- attr(*, "names")= chr [1:5] "user.self" "sys.self" "elapsed" "user.child" ...
## - attr(*, "class")= chr "gfm"# select q automatically
gfm2 <- gfm(dat$X, group, type, q=NULL, q_set = 1:6, output = F)## The factor number q is estimated as 2 .
## Starting the alternate minimization algorithm...
## Finish the iterative algorithm...str(gfm2)## List of 6
## $ hH : num [1:100, 1:2] 0.198 -0.324 0.47 0.653 0.317 ...
## $ hB : num [1:100, 1:2] 0.1963 -0.169 0.1607 -0.4243 -0.0848 ...
## $ hmu : num [1:100] 0.259 0.684 0.638 -0.191 -0.877 ...
## $ obj : num 0.966
## $ q : int 2
## $ history:List of 7
## ..$ dB : num [1:3] 1 0.01765 0.00541
## ..$ dH : num [1:3] 0.0558 0.01407 0.00493
## ..$ dc : num [1:3] 1.00 1.13e-04 6.29e-05
## ..$ c : num [1:3] 0.966 0.966 0.966
## ..$ realIter : num 3
## ..$ maxIter : num 50
## ..$ elapsedTime: 'proc_time' Named num [1:5] 0.12 0.1 2.14 NA NA
## .. ..- attr(*, "names")= chr [1:5] "user.self" "sys.self" "elapsed" "user.child" ...
## - attr(*, "class")= chr "gfm"# measure the performance of GFM estimators
measurefun(gfm2$hH, dat$H0, type='ccor')## [1] 0.8977694measurefun(gfm2$hB, dat$B0, type='ccor')## [1] 0.9185544In the above commands, we require to specify the types of each variables by parameters group and type. At the same time, we can speficy the number of factors to be extracted or let it be automatically selected by PC(IC) criteria. ### Heterogeous continuous variables In this exmaple, we generate data with heterogeous normal variables from the following model \[x_{ij}= \mu_j + h_i b_j^T + u_{ij},\] ,where \(u_{ij} \sim N(0, \sigma_j^2)\), which can be generated by function gendata:
n <- 100
p <- 100
q <- 2; rho <- 4
type <- 'heternorm'
dat <- gendata(seed=1, n=n, p=p, type= type, q=q, rho=rho)
str(dat)## List of 4
## $ X : num [1:100, 1:100] 0.699 -2.001 1.645 0.152 3.115 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : NULL
## .. ..$ : NULL
## $ B0 : num [1:100, 1:2] 0.2655 -0.0778 0.3542 -0.6761 -0.1397 ...
## $ H0 : num [1:100, 1:2] -0.148658 -0.000162 -0.098823 1.02493 0.628709 ...
## $ mu0: num [1:100] 0.164 0.676 0.635 -0.132 -0.914 ...group <- rep(1,ncol(dat$X))
type <- 'gaussian'
gfm3 <- gfm(dat$X, group, type, q=NULL, q_set = 1:4, output = F)## The factor number q is estimated as 2 .
## Starting the alternate minimization algorithm...
## Finish the iterative algorithm...plot(gfm3$history$dc, type='o')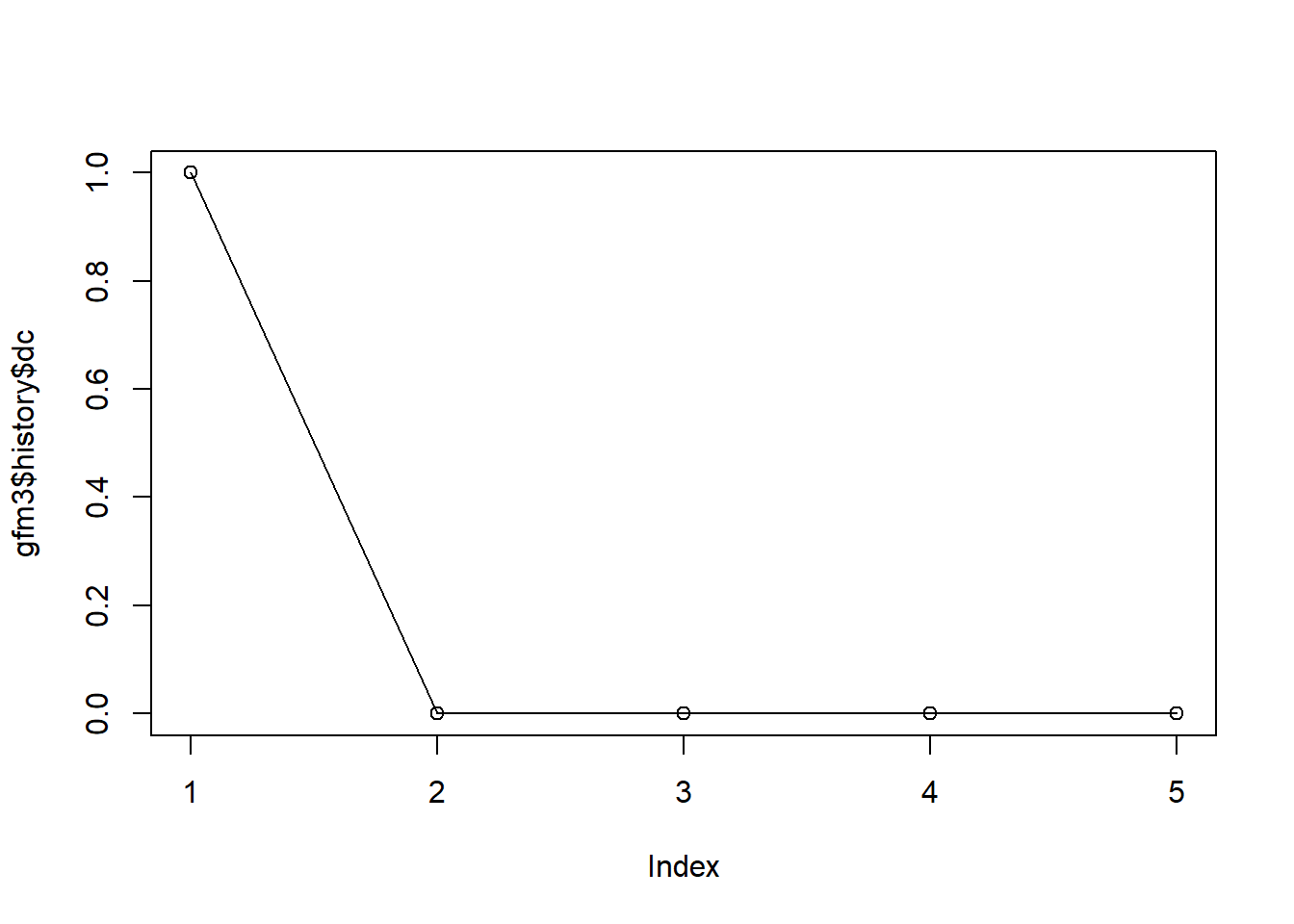
We compare the performance with the linear factor model by using functions measurefun and Factorm, where the measure of cononical correlation is used. The larger its value, the better.
measurefun(gfm3$hH, dat$H0, type='ccor')## [1] 0.9560164measurefun(gfm3$hB, dat$B0, type='ccor')## [1] 0.9274218Fac <- Factorm(dat$X)
measurefun(Fac$hH, dat$H0, type='ccor')## [1] 0.8904272measurefun(Fac$hB, dat$B0, type='ccor')## [1] 0.8970445The above results show that GFM can produce better estimators by using the information of heterogeous variances.